Introduction

Simulate from a Gaussian copula and use mixed-normal distributions as margins

In [1]: import numpy as np

In [2]: from scipy.stats import multivariate_normal, norm, invwishart

In [3]: from scipy.linalg import toeplitz

In [4]: from scipy.optimize import root_scalar

In [5]: class GaussianMixture:
   ...:     def __init__(self, weights, mus, sigmas):
   ...:         self.weights = weights
   ...:         self.mus = mus
   ...:         self.sigmas = sigmas
   ...:         self.n_components = len(weights)
   ...:     def cdf(self, x):
   ...:         res = np.zeros_like(x)
   ...:         for i_component in range(self.n_components):
   ...:             res += self.weights[i_component] * norm.cdf(x,
   ...:                                                         loc=self.mus[i_component],
   ...:                                                         scale=self.sigmas[i_component])
   ...:         return res
   ...:     def ppf(self, x):
   ...:         bracket = [-10., 10.]
   ...:         if x.min() < self.cdf(bracket[0:1]):
   ...:             bracket[0] -= 50.
   ...:         if x.max() > self.cdf(bracket[1:2]):
   ...:             bracket[1] += 50.
   ...:         res = np.array([root_scalar(lambda yy: self.cdf(np.array([[yy]]).T) - x[i],
   ...:                                     bracket=bracket,
   ...:                                     method='brentq',
   ...:                                     xtol=1e-12, rtol=1e-12).root for i in range(len(x))])
   ...:         return res
   ...: 

In [6]: n_vars = 5

In [7]: margins = [None]*n_vars

In [8]: for i_var in range(n_vars):
   ...:     n_components = 3
   ...:     weights = np.full(n_components, 1./n_components)
   ...:     mus = norm.rvs(size=n_components, scale=2.)
   ...:     sigmas = np.sqrt(invwishart.rvs(df=3, scale=1.0, size=n_components))
   ...:     margins[i_var] = GaussianMixture(weights, mus, sigmas)
   ...: 

In [9]: cov_mat = toeplitz([np.power(0.5, k) for k in range(5)])

In [10]: u_train = norm.cdf(multivariate_normal(mean=np.zeros(5), cov=cov_mat).rvs(1000))

In [11]: x_train = np.full_like(u_train, np.nan)

In [12]: for i_var in range(n_vars):
   ....:     x_train[:, i_var] = margins[i_var].ppf(u_train[:, i_var])
   ....: 

In [13]: u_test = norm.cdf(multivariate_normal(mean=np.zeros(5), cov=cov_mat).rvs(1000))

In [14]: x_test = np.full_like(u_test, np.nan)

In [15]: for i_var in range(n_vars):
   ....:     x_test[:, i_var] = margins[i_var].ppf(u_test[:, i_var])
   ....: 

Gaussian knockoffs

Estimate a Gaussian knockoff model

In [16]: from vineknockoffs.vine_knockoffs import VineKnockoffs

In [17]: gau_ko = VineKnockoffs()

In [18]: gau_ko.fit_gaussian_knockoffs(x_train=x_train)
Out[18]: <vineknockoffs.vine_knockoffs.VineKnockoffs at 0x7f13502b9a30>

In [19]: gau_ko._dvine.copulas
Out[19]: 
[[GaussianCopula(par=[0.4489001]),
  GaussianCopula(par=[0.48167758]),
  GaussianCopula(par=[0.50485079]),
  GaussianCopula(par=[0.51236845]),
  GaussianCopula(par=[0.08826382]),
  GaussianCopula(par=[0.4489001]),
  GaussianCopula(par=[0.48167758]),
  GaussianCopula(par=[0.50485079]),
  GaussianCopula(par=[0.51236845])],
 [GaussianCopula(par=[0.02854314]),
  GaussianCopula(par=[-0.00969086]),
  GaussianCopula(par=[0.01166561]),
  GaussianCopula(par=[0.14039401]),
  GaussianCopula(par=[0.07991839]),
  GaussianCopula(par=[0.02854314]),
  GaussianCopula(par=[-0.00969086]),
  GaussianCopula(par=[0.01166561])],
 [GaussianCopula(par=[0.06233617]),
  GaussianCopula(par=[-0.01899161]),
  GaussianCopula(par=[0.18216914]),
  GaussianCopula(par=[0.16629839]),
  GaussianCopula(par=[0.24476181]),
  GaussianCopula(par=[0.06233617]),
  GaussianCopula(par=[-0.01899161])],
 [GaussianCopula(par=[0.01043043]),
  GaussianCopula(par=[0.39365313]),
  GaussianCopula(par=[0.39891868]),
  GaussianCopula(par=[0.40050723]),
  GaussianCopula(par=[0.45250961]),
  GaussianCopula(par=[0.01043043])],
 [GaussianCopula(par=[-0.25828746]),
  GaussianCopula(par=[-0.22723834]),
  GaussianCopula(par=[-0.08053081]),
  GaussianCopula(par=[-0.07758852]),
  GaussianCopula(par=[-0.35665741])],
 [GaussianCopula(par=[0.64614131]),
  GaussianCopula(par=[0.54497431]),
  GaussianCopula(par=[0.46927182]),
  GaussianCopula(par=[0.71024124])],
 [GaussianCopula(par=[-0.55794148]),
  GaussianCopula(par=[-0.38227897]),
  GaussianCopula(par=[-0.48864249])],
 [GaussianCopula(par=[0.64844621]), GaussianCopula(par=[0.41442168])],
 [GaussianCopula(par=[-0.99475601])]]

Generate a knockoff copy

In [20]: x_gau_ko = gau_ko.generate(x_test)

Pairwise scatter plots

In [21]: import pandas as pd

In [22]: import seaborn as sns

In [23]: import matplotlib.pyplot as plt

In [24]: sns.set(font_scale=1)

In [25]: sns.pairplot(pd.DataFrame(np.hstack((x_test, x_gau_ko))))
Out[25]: <seaborn.axisgrid.PairGrid at 0x7f1348f55cd0>

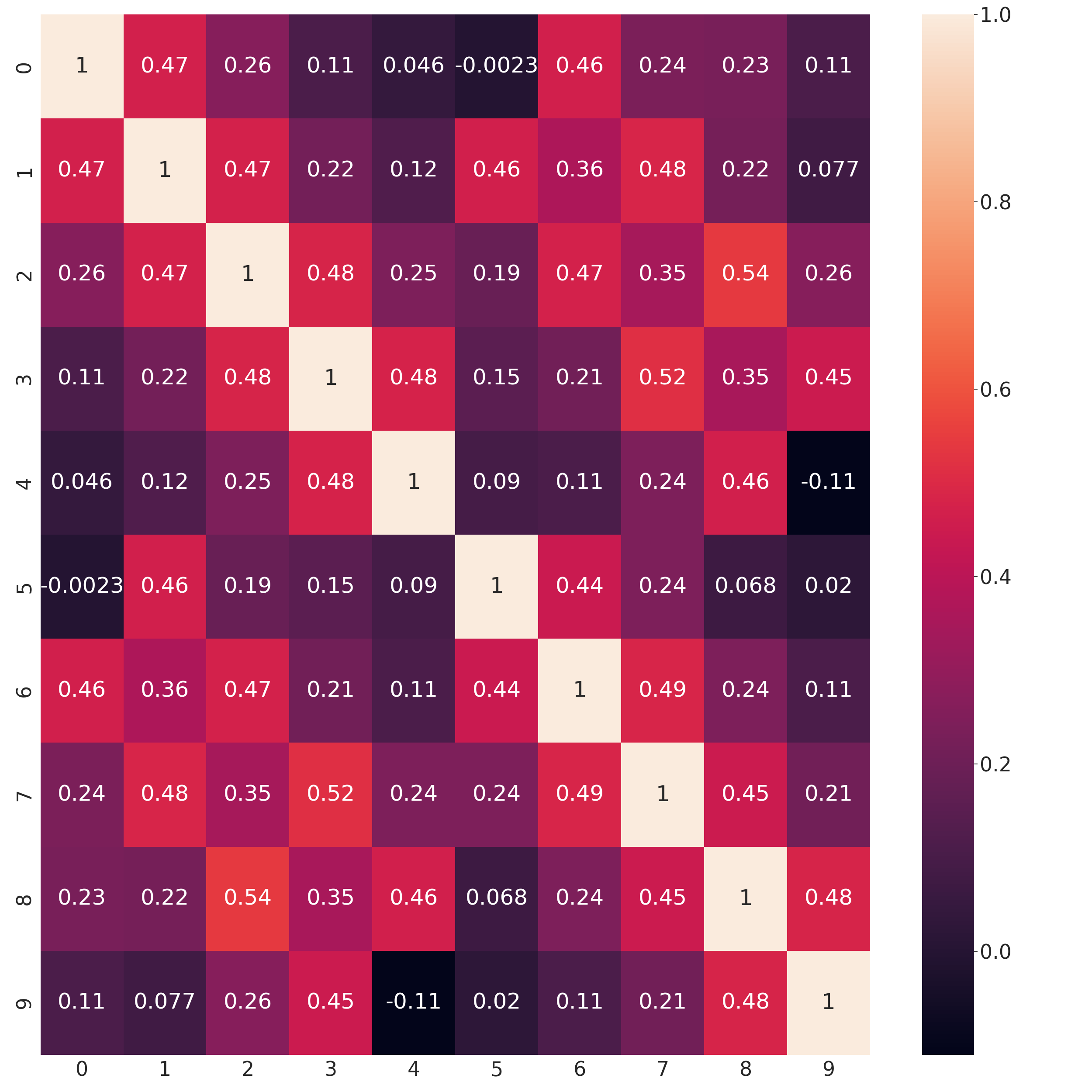
Estimated correlations

In [26]: sns.set(font_scale=3)

In [27]: sns.heatmap(np.corrcoef(np.hstack((x_test, x_gau_ko)).T), annot=True);

Gaussian copula knockoffs

Estimate a Gaussian copula knockoff model

In [28]: from vineknockoffs.vine_knockoffs import VineKnockoffs

In [29]: gau_cop_ko = VineKnockoffs()

In [30]: gau_cop_ko.fit_gaussian_copula_knockoffs(x_train=x_train)
Out[30]: <vineknockoffs.vine_knockoffs.VineKnockoffs at 0x7f1347498760>

In [31]: gau_cop_ko._dvine.copulas
Out[31]: 
[[GaussianCopula(par=[0.49889927]),
  GaussianCopula(par=[0.51485352]),
  GaussianCopula(par=[0.51563259]),
  GaussianCopula(par=[0.51825192]),
  GaussianCopula(par=[0.08920866]),
  GaussianCopula(par=[0.49889927]),
  GaussianCopula(par=[0.51485352]),
  GaussianCopula(par=[0.51563259]),
  GaussianCopula(par=[0.51825192])],
 [GaussianCopula(par=[-0.00416141]),
  GaussianCopula(par=[-0.01605925]),
  GaussianCopula(par=[0.00478767]),
  GaussianCopula(par=[0.15206381]),
  GaussianCopula(par=[0.09216385]),
  GaussianCopula(par=[-0.00416141]),
  GaussianCopula(par=[-0.01605925]),
  GaussianCopula(par=[0.00478767])],
 [GaussianCopula(par=[0.06845161]),
  GaussianCopula(par=[-0.01260832]),
  GaussianCopula(par=[0.19342715]),
  GaussianCopula(par=[0.17230366]),
  GaussianCopula(par=[0.24343657]),
  GaussianCopula(par=[0.06845161]),
  GaussianCopula(par=[-0.01260832])],
 [GaussianCopula(par=[0.00267909]),
  GaussianCopula(par=[0.44566922]),
  GaussianCopula(par=[0.43046756]),
  GaussianCopula(par=[0.4090201]),
  GaussianCopula(par=[0.45793907]),
  GaussianCopula(par=[0.00267909])],
 [GaussianCopula(par=[-0.33754818]),
  GaussianCopula(par=[-0.00999287]),
  GaussianCopula(par=[-0.11597554]),
  GaussianCopula(par=[-0.0109706]),
  GaussianCopula(par=[-0.36733475])],
 [GaussianCopula(par=[0.63963203]),
  GaussianCopula(par=[0.48851243]),
  GaussianCopula(par=[0.46462707]),
  GaussianCopula(par=[0.68064834])],
 [GaussianCopula(par=[-0.5505026]),
  GaussianCopula(par=[-0.33889836]),
  GaussianCopula(par=[-0.46158122])],
 [GaussianCopula(par=[0.63887789]), GaussianCopula(par=[0.37102548])],
 [GaussianCopula(par=[-0.99548401])]]

Generate a knockoff copy

In [32]: x_gau_cop_ko = gau_cop_ko.generate(x_test)

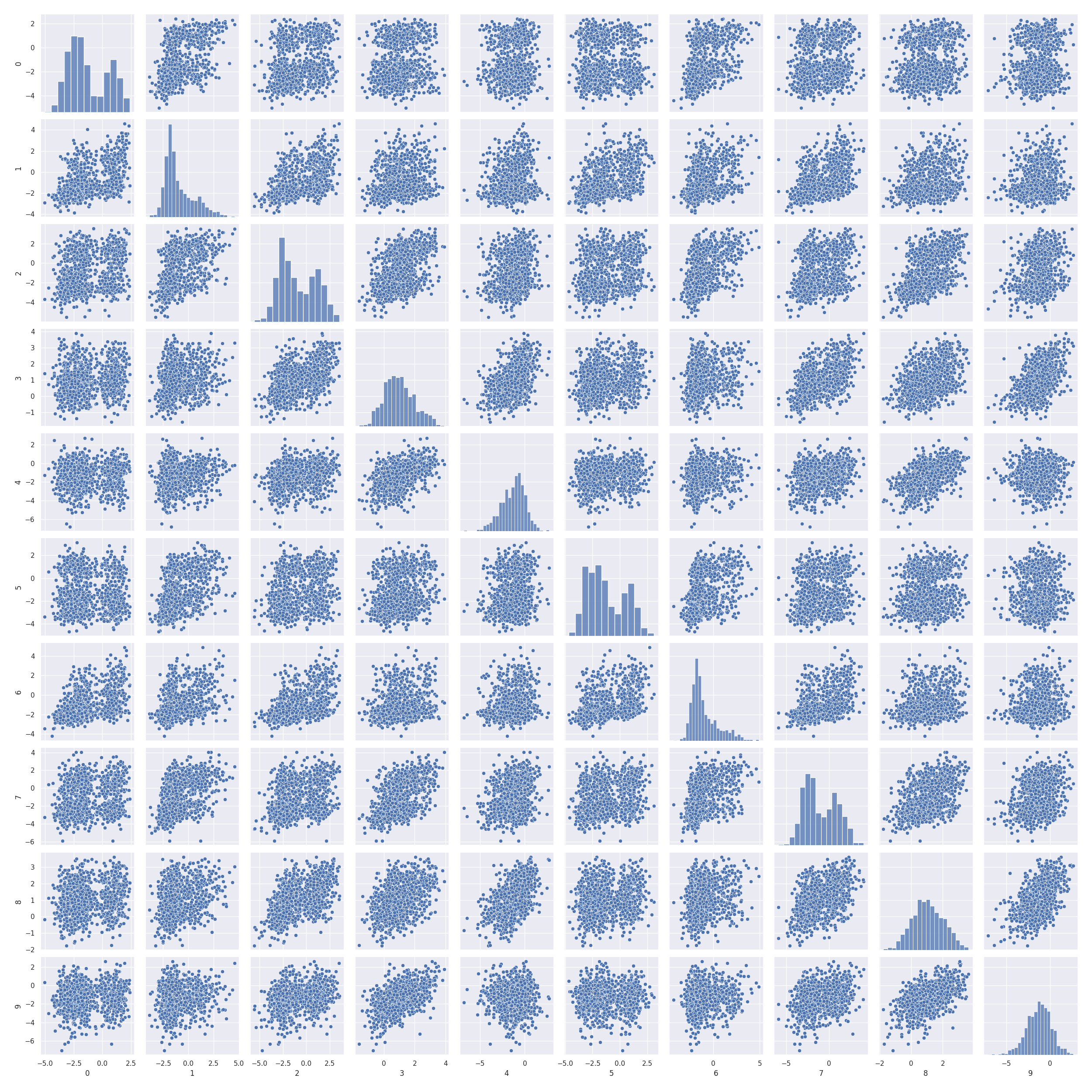
Pairwise scatter plots

In [33]: import pandas as pd

In [34]: import seaborn as sns

In [35]: import matplotlib.pyplot as plt

In [36]: sns.set(font_scale=1)

In [37]: sns.pairplot(pd.DataFrame(np.hstack((x_test, x_gau_cop_ko))))
Out[37]: <seaborn.axisgrid.PairGrid at 0x7f1347b128e0>

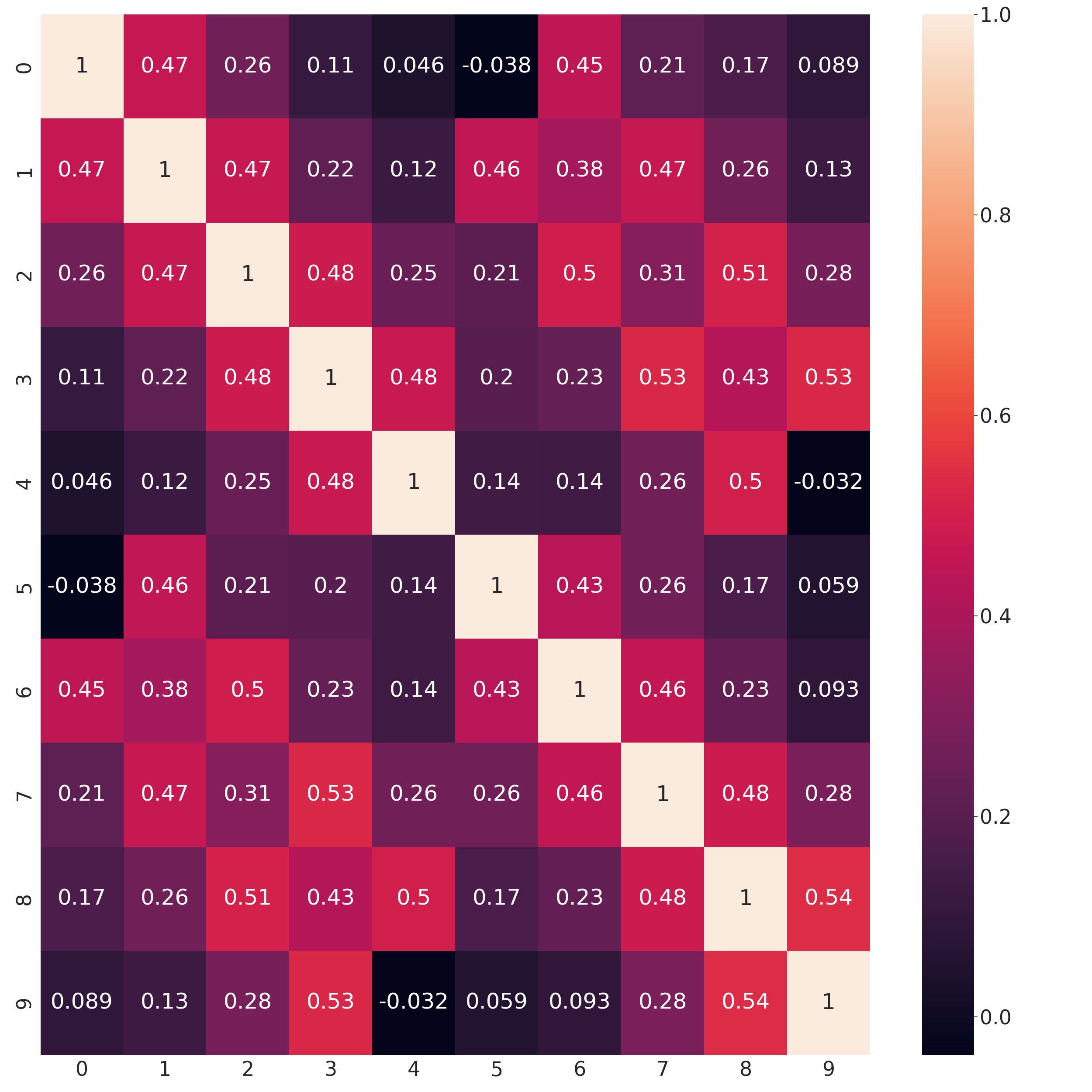
Estimated correlations

In [38]: sns.set(font_scale=3)

In [39]: sns.heatmap(np.corrcoef(np.hstack((x_test, x_gau_cop_ko)).T), annot=True);

Vine copula knockoffs

Estimate a Gaussian copula knockoff model

In [40]: from vineknockoffs.vine_knockoffs import VineKnockoffs

In [41]: vine_ko = VineKnockoffs()

In [42]: vine_ko.fit_vine_copula_knockoffs(x_train=x_train)
Out[42]: <vineknockoffs.vine_knockoffs.VineKnockoffs at 0x7f13447aa490>

In [43]: vine_ko._dvine.copulas
Out[43]: 
[[GaussianCopula(par=[0.48383016]),
  GaussianCopula(par=[0.51726826]),
  GaussianCopula(par=[0.27181872]),
  GaussianCopula(par=[0.51290159]),
  GaussianCopula(par=[0.16647727]),
  GaussianCopula(par=[0.48383016]),
  GaussianCopula(par=[0.51726826]),
  GaussianCopula(par=[0.27181872]),
  GaussianCopula(par=[0.51290159])],
 [IndepCopula(),
  IndepCopula(),
  GaussianCopula(par=[0.45121434]),
  IndepCopula(),
  GaussianCopula(par=[0.19896423]),
  IndepCopula(),
  IndepCopula(),
  GaussianCopula(par=[0.45121434])],
 [IndepCopula(),
  IndepCopula(),
  ClaytonCopula(par=[0.22514369], rotation=180),
  IndepCopula(),
  GaussianCopula(par=[0.46917166]),
  IndepCopula(),
  IndepCopula()],
 [IndepCopula(),
  GaussianCopula(par=[0.44616686]),
  GaussianCopula(par=[0.43643683]),
  IndepCopula(),
  GaussianCopula(par=[0.45584443]),
  IndepCopula()],
 [GaussianCopula(par=[-0.33754818]),
  GaussianCopula(par=[-0.00999287]),
  GaussianCopula(par=[-0.11597554]),
  GaussianCopula(par=[-0.36733475]),
  GaussianCopula(par=[-0.0109706])],
 [GaussianCopula(par=[0.63963203]),
  GaussianCopula(par=[0.48851243]),
  GaussianCopula(par=[0.01680553]),
  GaussianCopula(par=[0.68064834])],
 [GaussianCopula(par=[-0.5505026]),
  GaussianCopula(par=[-0.03065251]),
  GaussianCopula(par=[0.61868149])],
 [GaussianCopula(par=[0.0467642]), GaussianCopula(par=[-0.48578146])],
 [GaussianCopula(par=[0.99732389])]]

Generate a knockoff copy

In [44]: x_vine_ko = vine_ko.generate(x_test)

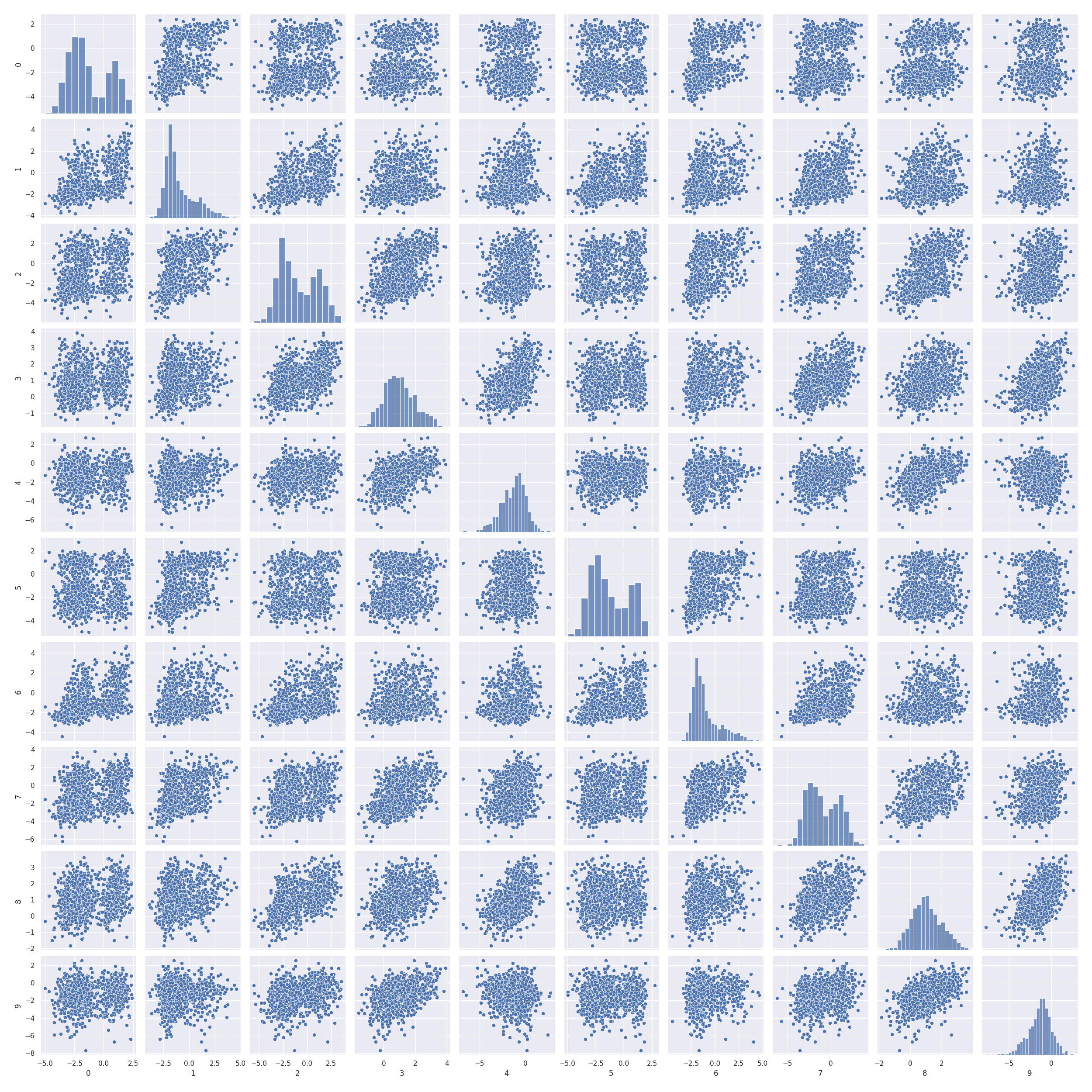
Pairwise scatter plots

In [45]: import pandas as pd

In [46]: import seaborn as sns

In [47]: import matplotlib.pyplot as plt

In [48]: sns.set(font_scale=1)

In [49]: sns.pairplot(pd.DataFrame(np.hstack((x_test, x_vine_ko))))
Out[49]: <seaborn.axisgrid.PairGrid at 0x7f1344bc5df0>

Estimated correlations

In [50]: sns.set(font_scale=3)

In [51]: sns.heatmap(np.corrcoef(np.hstack((x_test, x_vine_ko)).T), annot=True);